Tạo chứng thư số Self-Sign Certificate ^runable

Giới thiệu

Chữ ký số (CKS) là một dạng của [chữ ký điện tử] https://en.wikipedia.org/wiki/Electronic_signature). Nó là một dạng dữ liệu dùng để chứng thực cho các dữ liệu khác. Để tạo chữ ký số cho 1 tài liệu, ta cần sử dụng chứng thư số (Certificate).

Nếu chữ ký số tương đương với chữ ký trên giấy thì chứng thư số tương đương với cái bút đặc biệt để ký ra chữ ký số đó.

Chữ ký số được nhà nước công nhận và có giá trị pháp lý nếu chứng thư số (Certificate) sử dụng để ký được phát hành bởi các đơn vị cung cấp Certificate được nhà nước cấp phép.

Trong phạm vi nội bộ công ty. Ta có thể tự tạo và sử dụng chứng thư số (Certificate) mà không cần mua của các nhà phát hành bên ngoài. Nếu ta được nhà nước cấp phép. Nhà nước sẽ cấp 1 Certificate master. Ta dùng Certificate master để tạo ra các chứng thư số, thì chúng có giá trị pháp lý và bán lấy tiền được.

Tính năng này cho phép tạo ra X509 certificate. Certificate có thể dùng để

Mã hóa nội dung text,
Mã hóa văn bản theo thuật toán bất đối xứng. Hacker dùng thuật toán này để chạy ransomware mã hóa lén lút các file của nạn nhân để đòi tiền chuộc.
Ký số văn bản, hóa đơn, hợp đồng.

Để tạo Certtificate được issue bởi SPC Technology. Xem thêm lệnh SPC.Crypto.Commands.IssueCertificate

Sử dụng

SPC.Crypto.Commands.SelfSignCert?name=Cert_Name&password = secret

name: Tên người hoặc công ty sử dụng CKS
password: Mật khẩu để sử dụng private key khi mã hóa hoặc ký.

Certificate được tạo ra có public key và private key. Password được dùng để sử dụng private key. Nếu quên password thì certificate không thể sử dụng để ký số hoặc giải mã được nữa.

Nếu không cung cấp name và password, chương trình sẽ hỏi tên của người hoặc công ty sử dụng CKS

Chương trình sẽ tạo certificate và lưu dưới định dạng pkcs12 ở trong My Documents\Backup\ folder.

ade305c0-c1fe-4fee-94c2-c1ebe67d6098.spc_crypto_commands_selfsigncert_md

Ta có 2 cách sử dụng Certificate này để ký văn bản.

Double Click vào Certificate và import vào windows certificate manager.

dd047a32-9608-4509-9bdd-f58936ae4bb2.spc_crypto_commands_selfsigncert_md
58b837c1-6c9d-4963-88ef-42b10de20355.spc_crypto_commands_selfsigncert_md

Tạo 1 mẩu tin PKCS#12 Storage và tải Certificate này vào.

Sau khi thực hiện 1 trong 2 bước này thì Certificate có thể sử dụng để ký văn bản hoặc mã hóa.

Mã hóa bất đối xứng RSA

RSA là gì?

Thuật toán RSA được Ron Rivest, Adi Shamir và Len Adleman mô tả lần đầu tiên vào năm 1977 tại Học viện Công nghệ Massachusetts (MIT).

RSA là lấy từ chữ cái đầu tiên của tên 3 tác giả. Đây là một thuật toán mật mã hóa khóa công khai. Thuật toán RSA là thuật toán đầu tiên phù hợp với việc tạo ra chữ ký điện tử bằng việc mã hóa.

Đối với lĩnh vực mật mã học thì RSA là một sự tiến bộ vượt bậc trong việc sử dụng khóa công cộng. Nó đang được ứng dụng rộng rãi trong thương mại điện tử.

Thuật toán RSA được MIT đăng ký bằng sáng chế tại Hoa Kỳ vào năm 1983 (Số đăng ký 4.405.829).

Hệ thống mã hoá RSA bao gồm 4 bước: key generation, key distribution, encryption và decryption. Mỗi hệ thống khác nhau cần tạo ra các public và private key khác nhau để đảm bảo tính bí mật.

Sơ lược về mã hoá đối xứng và bất đối xứng:

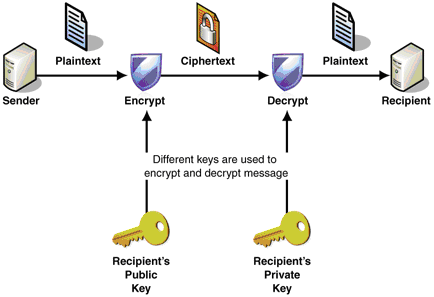
Trong lĩnh vực an toàn thông tin có hai loại mã hoá phổ biến là: mã hoá đối xứng (symmetric cryptography) và mã hoá bất đối xứng (asymmetric cryptography).

Cụ thể:

Mã hoá đối xứng (mã hoá bí mật): Có nghĩa là – Bạn có một chìa khoá nhưng có thể dùng để khoá và mở thông tin. Cả bên gửi và bên nhận thông tin đều cần phải có chìa khoá này.
Mã hoá bất đối xứng (mã hoá công khai): Có nghĩa là – Bạn cần phải dùng hai chìa khoá khác nhau để khoá và mở khoá thông tin. public key sẽ được công khai và private key được giữ bí mật, nó có thể mở được tất cả thông tin được khoá bằng public key.

Tại sao cần mã hoá bất đối xứng?

Hầu hết các website hiện nay như: Facebook, google, youtube,… đều sử dụng giao thức HTTPs. Có thể hiểu là giao thức HTTPs an toàn hơn HTTP vì toàn bộ thông tin truyền đi giữa client và server được bảo vệ bởi bộ mã hoá SSL/TSL. SSL/TSL này hoạt động dựa trên cả hai loại mã hoá đối xứng và bất đối xứng.

Nhờ đó mà chúng ta có thể đảm bảo bí mật thông tin trên Internet mà không bị đánh cắp thông tin trong quá trình truyền nhận dữ liệu. Có thể nói, nếu không có mã hoá bất đối xứng thì không có thương mại điện tử.

Cách tạo public và private key

Mấu chốt cơ bản của việc sinh khóa trong RSA là tìm được bộ 3 số tự nhiên e, d và n sao cho:

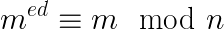
và một điểm không thể bỏ qua là cần bảo mật cho d sao cho dù biết e, n hay thậm chí cả m cũng không thể tìm ra d được.

Cụ thể, khóa của RSA được sinh như sau:

Chọn 2 số nguyên tố p và q
Tính n = pq. Sau này, n sẽ được dùng làm modulus trong cả public key và private key.
Tính một số giả nguyên tố bằng phi hàm Carmichael như sau: λ(n) = BCNN(λ(p), λ(q)) = BCNN(p − 1, q − 1). Giá trị này sẽ được giữ bí mật.
Chọn một số tự nhiên e trong khoảng (1, λ(n)) sao cho ƯCLN(e, λ(n)) = 1, tức là e và λ(n) nguyên tố cùng nhau.
Tính toán số d sao cho d ≡ 1/e (mod λ(n)) hay viết dễ hiểu hơn thì de ≡ 1 (mod λ(n)). Số d được gọi là số nghịch đảo modulo của e (theo modulo mod λ(n)).

Public key sẽ là bộ số (n, e), và private key sẽ là bộ số (n, d). Chúng ta cần giữ private key thật cẩn thận cũng như các số nguyên tố p và q vì từ đó có thể tính toán các khóa rất dễ dàng.

Trong thực hành, chúng ta thường chọn e tương đối nhỏ để việc mã hóa và giải mã nhanh chóng hơn. Giá trị thường được sử dụng là e = 65537.

Ngoài ra, chúng ta có thể tính số giả nguyên tố bằng phi hàm Euler φ(n) = (p − 1)(q − 1) và dùng nó như λ(n). Vì φ(n) là bội của λ(n) nên các số d thỏa mãn de ≡ 1 (mod φ(n)) cũng sẽ thỏa mãn d ≡ 1/e (mod λ(n)). Tuy nhiên, một số tác dụng phụ của việc này là d thường sẽ trở nên lớn hơn mức cần thiết.

8beae7e1-9b89-4d60-ad2b-6cfee8d78a94.spc_crypto_commands_selfsigncert_md

Mã hóa và giải mã

Trong phần này, chúng ta sẽ tìm hiểu cách mã hóa với public key (n, e) và giải mã với private key (n, d). Nếu chúng ta có bản rõ M, chúng ta cần chuyển nó thành một số tự nhiên m trong khoảng (0, n) sao cho m, n nguyên tố cùng nhau. Việc này rất dễ dàng thực hiện bằng cách thêm một các kỹ thuật padding. Tiếp theo, chúng ta sẽ má hóa m, thành c như sau:

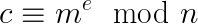
Sau đó giá trị c sẽ được chuyển cho người nhận.

Ở phía người nhận, họ sẽ giải mã từ c để lấy được m như sau:

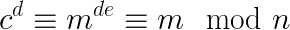
Từ m có thể lấy lại được bản tin bằng cách đảo ngược padding

Chúng ta lấy một ví dụ đơn giản như sau:

p = 5, q = 7 => n = pq = 35  => φ(n) = 24

Chúng ta chọn e = 5 vì ƯCLN(5, 24) = 1, cuối cùng chọn d = 29 vì ed - 1 = 29x5 - 1 chia hết cho 24. Giả sử m = 32 (dấu cách), chúng ta sẽ mã hóa m và thu được c = 32 ^ 5 % 35 = 2

Giải mã c để thu được m : m = 2 ^ 29 % 35 = 32

Đây chính là m ban đầu. Bạn có thể thứ m với các giá trị khác nhau để thấy thuật toán hoàn toàn chính xác. Tất nhiên rồi, nó đã được chứng minh mà. Việc chứng minh RSA hoạt động chính xác là một vấn đề toán học khá phức tạp mà bài viết này sẽ không đi vào chi tiết của nó.

1e9ba853-a47e-46b3-b538-1a70ec8a9a27.spc_crypto_commands_selfsigncert_md

Mức độ bảo mật của RSA phụ thuộc rất lớn vào khả năng phân tích thừa số nguyên tố của các số lớn. Bởi vì chúng ta cung cấp public một cách rộng rãi, nếu việc phân tích thừa số nguyên tố đơn giản, thì việc bị lộ private là không thể tránh khỏi.

Vì vậy, khi sinh khóa, chúng ta cần chọn các số nguyên tố p và q một cách ngẫu nhiên. Bản thân hai số nguyên tố này cũng rất lớn, và để việc phân tích thừa số nguyên tố khó khăn hơn, hai số nguyên tố này sẽ không có cùng độ dài. Trong tương lai gần, có lẽ vẫn chưa có một phương pháp hiệu quả nào cho phép thực hiện điều này với các máy tính cá nhân.

Chữ ký số sử dụng hệ mã hóa RSA

Việc ký tên và xác thực chữ ký số sử dụng hệ mã hóa RSA tương tự như quá trình mã hóa mà giải mã ở trên. Tuy nhiên vai trò của public key và private thì có thay đổi đôi chút.

Để tạo chữ ký, người gửi sẽ dùng private key và người nhận sẽ dùng public key để xác thực chữ ký đó. Tuy nhiên, vì bản tin rất dài nên việc mã hóa toàn bộ bản tin sẽ rất mất thời gian. Vì vậy, trong thực hành, chữ ký số thường sử dụng phương pháp mã hóa giá trị hash của bản tin. Việc này mang lại rất nhiều lợi ích như:

Các hàm hash là hàm 1 chiều, vì vậy dù có được hash cũng không thể biết được bản tin gốc như thế nào.
Độ dài hash là cố định và thường rất nhỏ, vì vậy chữ số sẽ không chiếm quá nhiều dung lượng.
Giá trị hash còn có thể dùng để kiểm tra lại bản tin nhận được có nguyên vẹn hay không?

7eec6657-b0bb-415a-ac1b-3a4d8a205bb0.spc_crypto_commands_selfsigncert_md

Chữ ký số đem lại nhiều giá trị hơn chữ ký tay rất nhiều. Có lẽ cũng vì vậy, việc xử lý chữ ký số phức tạp hơn hẳn chữ ký tay truyền thống:

1. Xác định nguồn gốc

Hệ mã hóa bất đối xứng cho phép tạo chữ ký với private key mà chỉ người chủ mới biết. Khi nhận gói tin, người nhận xác thực chữ ký bằng cách dùng public key giải mã, sau đó tính giá trị hash của bản tin gốc và so sánh với hash trong gói tin nhận được. Hai chuỗi này phải trùng khớp với nhau. Tất nhiêu hệ mã hóa RSA vẫn có những thách thức về an ninh nhất định nhưng dù sao thì nó vẫn khá an toàn.

2. Dữ liệu được giữ một cách toàn vẹn Tin nhắn gửi từ chủ private key rất khó có thể bị giả mạo. Bởi vì nếu thay đổi tin nhắn thì giá trị hash cũng phải thay đổi theo. Những kẻ nghe lén trong mạng đương nhiên là có thể tìm cách đọc tin nhắn gốc và cả hash của nó. Nhưng hắn ta không thể thay đổi tin nhắn được vì hắn không có private key để sửa đổi chữ ký số cho phù hợp.

3. Chữ ký số không thể phủ nhận Trong giao dịch, một gói tin kèm chữ ký số rất dễ dàng tìm ra được nguồn gốc của chữ ký đó. Bởi vì private key là bí mật và chỉ người chủ của nó mới có thể biết, họ không thể chối cãi rằng chữ ký này không phải do họ phát hành. Cũng tương tự trường hợp trên, hệ mã hóa RSA hay bất kỳ hệ mã hóa nào khác cũng đều có những vấn đề về an ninh nên việc này không thể đảm bảo tuyệt đối chính xác được.

Xem thêm

-SPC.Crypto.Commands.IssueCertificate

_{Updated on : 2021-07-31 00:43:49}. _{by : . at T470-01}.

_{Topic : . spc.crypto.commands.selfsigncert}

Tạo chứng thư số Self-Sign Certificate runable